Tag: matrix

XLA를 소개합니다.

최근 업무 관련해서 XLA를 알게 되었는데, 재밌는 프로젝트인데 반해 관련된 자료를 찾는게 쉽지 않길래 한번 소개를 해보면 좋을 것 같다는 생각이 들었습니다.

우선 XLA (Accelerated Linear Algebra)는 Tensorflow의 서브 프로젝트로 그래프 연산의 최적화 / 바이너리 사이즈의 최소화 등을 목적으로 하는 컴파일러입니다.

Continue reading XLA를 소개합니다.

Math: line fitting

만약 서로 다른 2개의 (x,y) 쌍을 가지고 있다면 아래와 같은 직선의 방정식을 계산해낼 수 있습니다.

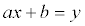
이를 아래와 같은 매트릭스 형태로 표현할 수도 있습니다.

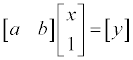
그런데 (x,y) 값을 2 쌍보다 더 많이 알고 있다면, 해가 구해낼 수 없게됩니다. 이를 over constraint 라고 하며, over constraint 상태에서 가장 에러가 작은 직선의 방정식을 구해내는 것을 line fitting 이라고 부릅니다.

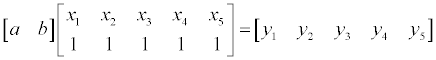
line fitting 을 하는 방법은 크게 2가지 방법이 있습니다. 첫번째는 에러를 최소화 하는 계수 a, b 를 찾기 위해 편미분을 이용하는 것이고, 두번째로는 pseudo inverse 를 이용하는 방법입니다.

line fitting with differencial equation

편미분을 통해 최적의 직선을 찾아내기 위해 우선 Error 를 아래와 같이 정의해 봅시다.

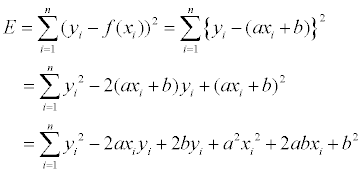
2차 곡선의 최소값은 기울기가 0이 되는 지점에 있으므로 a, b 각각에 대해 편미분을 한 뒤 기울기가 0 이 되는 지점을 찾습니다.

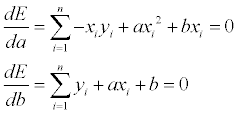
위 식을 정리하면 아래와 같은 매트릭스로 표현이 가능하며,

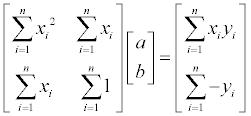
역함수를 양 변에 곱해주게 되면 간단히 계수 a, b 를 구할 수 있게 됩니다.

line fitting with pseudo inverse

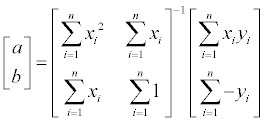
지금까지 편미분을 이용한 line fitting 을 알아봤는데, 이 경우는 손으로 계산해야하는 것들이 많았지만 pseudo inverse 를 이용하면 계산을 모두 컴퓨터에게 맡길 수 있기 때문에 훨씬 쉽게 직선의 방정식을 구할 수 있습니다.

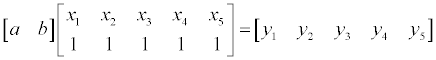
pseudo inverse 를 이용한 방법을 알아보기 앞서 위 매트릭스를 간단히 아래와 같이 표현하기로 하겠습니다.

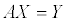
X 에 대한 inverse 를 계산할 수 있다면 간단하게 계수 a, b 를 구할 수 있겠지만 불행히도 X 는 inverse 를 가지지 못하기 때문에 X 에 자신의 transpose 를 곱해준 뒤 역행렬을 구하는 방법을 사용하게 되며, 이런 식으로 역행렬을 구해내는 방법을 pseudo inverse 라고 합니다.

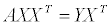
식을 정리하고 나니 아래와 같은 간단한(?) 행렬 연산을 통해 계수 a, b 를 계산해낼 수 있겠습니다.

Result

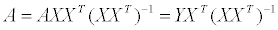
아래 그래프는 (1.1,0.7), (2.1,1.0), (4.3,3.2), (-1.2,-1.1), (-2.4,-2.1), (-3.5,-3.4) 이렇게 6개의 점에 대한 line fitting 결과를 gnuplot 을 이용해서 그래프로 만든 것이며, 6개의 점 사이를 지나는 직선이 구해진 것을 쉽게 확인할 수 있겠습니다.

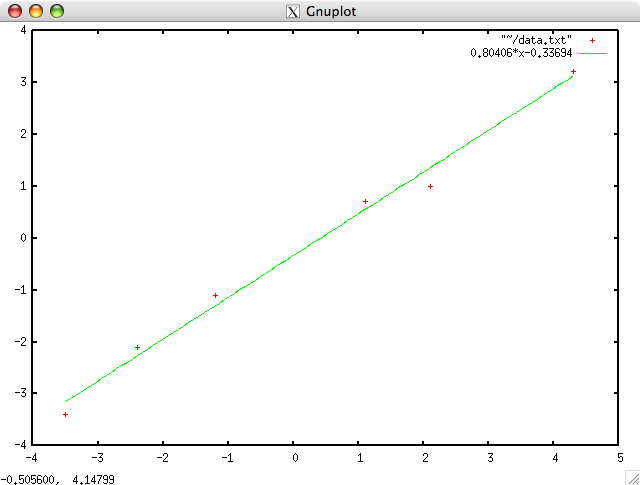
p.s) 매트릭스 관련된 오퍼레이션들을 다 짜놨더니 이거이거 이런 간단한 것들 돌려보는건 일도 아니네요. 요 근래 뭔가 조급해하고 있었는데, 맘잡고 기초부터 탄탄히 해놓는게 나을 거 같다는 생각이 들어서. 욕심을 줄이고 있습니다. 후훗

코드: https://github.com/Tee0125/linear_regression/blob/master/numpy/numpy_linear_regression.py

CG: 3D Image Rotation

며칠 전 Perspective Projection 을 정리해놓은 김에 3D Image Rotation 도 정리를 해볼까 싶습니다.

Rotation Matrix

3D 이미지 회전은 아래와 같은 행렬을 통해 새로운 좌표를 계산할 수 있습니다. 또한 이 행렬들은 모두 unitary matrix 이기 때문에 Transpose 를 취해줌으로 역행렬을 쉽게 구할 수 있습니다.

z축 기준: (xy 평면에서의 회전)

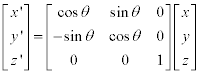
y축 기준: (zx 평면에서의 회전)

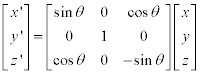
x축 기준: (yz 평면에서의 회전)

Implementation of Image Rotation

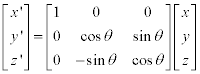
처음에는 3차원 공간을 3차원 배열을 사용하여 모델링한 뒤 실제 3차원 좌표를 모두 뒤지며 forward/backward mapping 하는 방법을 통해 3D image rotation 을 구현해보았습니다. 3차원 배열을 이용 512×512 사이즈의 lena image 를 회전시키려면 (512*1.414)^3 만큼의 공간이 필요하게 되고, 저 공간을 모두 뒤지려면 계산 복잡도가 엄청나더군요.

실제 이 방법을 통해 이미지를 회전 시키는 데 ‘분’ 단위 시간이 필요했던 것으로 기억합니다. 게다가 변환을 반복할 수록 이미지의 디그라데이션이 심해졌기 때문에 이건 아니라는 생각이 들더군요. 이런 경우 이미 잘 설계되어 있는 그래픽 라이브러리를 참고하는 것이 좋기 때문에 OpenGL 의 인터페이스를 살펴보며 어떤 식으로 구현하면 좋을 지 생각하기 시작했습니다.

뭐 어짜피 화면이나 이미지로 보여주기 위해선 2D 평면에 projection 하는 것이 필요하므로 매 번 이미지 자체를 돌리기 보다 축을 회전시키고, 마지막에 그 축을 이용해서 원래 이미지를 새로운 좌표 공간으로 매핑시켜주면 되겠다는 결론을 얻었습니다.
우선 x, y, z 좌표를 identity matrix 로 표현한 뒤 R^T * AXIS 를 통해 새로운 축 AXIS’ 를 구할 수 있고, 회전을 시키고 싶은 만큼 위 연산을 반복해준 뒤 forward mapping 을 해주는 것으로 빠르고 훌륭한 품질을 보여주도록 구현하는걸 성공했습니다.

위 이미지는 512×512 사이즈의 lena 이미지를 z축을 기준으로 45도만큼 회전시킨 결과입니다. 왼 쪽은 단순히 forward mapping 을 해준 것이고 오른쪽은 weighted sum 을 이용해서 forward mapping 을 개선해준 것입니다.

결과적으로 Photoshop 등을 이용한 만큼 훌륭한 이미지를 얻어낼 수 있는 것을 확인할 수 있습니다.

Other Results

아래 이미지는 x 축, y축, z축을 기준으로 순서대로 30도씩 회전시킨 이미지입니다. 이런 식으로 계산을 하려면 순서를 뒤집어서 z축, y축, x 축 기준으로 30도씩 회전을 시켜주면 됩니다.

다음은 x축으로 30도, y축으로 60도 만큼 돌린 결과

실제 구현 코드에 관심이 있으신 분들은 아래 링크를 방문하시면 되겠습니다. 이런 걸 하나하나 구현해볼 때마다 느끼는 거지만 openGL 같은 라이브러리를 설계하신 분들은 상상하기 힘들 정도로 똑똑한 것 같아요.

소스:
https://github.com/Tee0125/snippet/tree/master/rotation3d

CG: Perspective Projection

HCI 과제 덕에 심심찮게 프로그래밍을 하게 되네요. 첫 과제 였던 3D rotation 관련을 구현하는 것도 상당히 흥미로웠지만, 두번째 과제인 Perspective Projection 를 구현하는 것은 정말 멋진 경험이었다고 생각합니다.

지난 며칠간 꽤나 재밌게 프로그래밍을 했던 관계로 블로그에도 살짝 정리해보는게 어떨까 하는 생각이 들었는데, 막상 쓸려니 내용이 잘 전해질지 의문이네요.

What is the Perspective Projection?

Perspective Projection 이란 아래의 왼쪽 이미지를 오른쪽 이미지 처럼 변화시키는 것을 얘기합니다. 꼭 저렇게 비뚜러진 이미지를 바로잡는것은 아니고, 이미지가 투영되는 면을 변화시키는 것이라고 생각하시면 됩니다.

이해를 돕기 위해 wikipedia 에서 이미지를 하나 가져왔습니다. 아래 이미지의 연보라색 면이 상이 맺히는 곳이라고 할 때, perspective transform 은 그 보라색 면을 이동시킨 것 같은 효과를 주기 위해 사용합니다.

How to get a projection matrix.

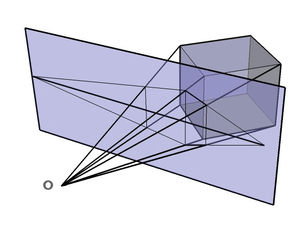
기본 적으로 Perspective Transform 을 위한 식은 다음과 같습니다.

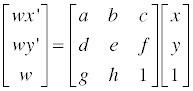
homogenious coordinate 를 사용하고 있으니 x’ 와 y’ 에 관한 식은 아래와 같이 바꿔쓸 수 있습니다.

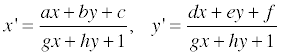
이를 정리하면 다음과 같은 꼴로 만들 수 있고,

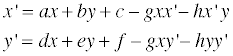
우리가 값을 알고 싶은 변수들은 a, b, c, d, e, f, g, h 이렇게 8 개이므로, (x, y) 와 그에 대응되는 (x’, y’) 쌍을 4개만 알고 있으면 projection matrix 를 구할 수 있습니다. 이를 구하기 위한 매트릭스는 아래와 같습니다.

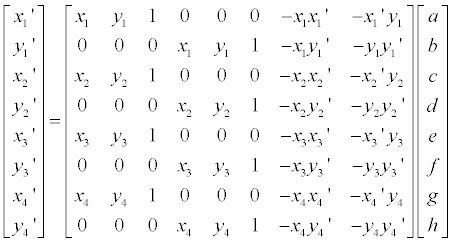
남은 건 8×8 matrix 의 inverse matrix 를 구한 뒤 뒤 쪽의 매트릭스에 곱해주는 것 뿐이군요.

Implementation of Perspective projection

이제까지 Perspective Transform 을 위한 매트릭스에 대해 알아봤습니다. 이제는 실제 구현을 해보는 것만 남았네요. 위에서 알아봤듯이 Perspective matrix 를 구하려면 matrix multiplication 과 inverse 를 위한 인터페이스가 필요합니다.

matrix multiplication 의 경우 서로 곱할 수 있는 형식인지를 체크한 뒤 단순한 계산을 하면 되고, inverse 는 gauss elimination 을 이용 reduced row echelon form 으로 만들어주는 것을 통해 쉽게(?) 구해낼 수 있습니다.

위의 두 가지까지 구현했다면, 이제 warping 만을 구현하면 되겠습니다. 이 warping 은 크게 두가지 방법을 통해 구현할 수 있습니다.

forward mapping

forward mapping 은 말 그대로 src 의 x, y 좌표에 대하 dst 의 x’, y’ 를 계산 한 뒤 값을 채워주는 방식입니다. 간단히 pseudo code 로 표현하면 다음과 같이 표현할 수 있겠네요.

근데 막상 구현을 해놓고 보면 pixel 이 정수단위이기 때문에 아래와 같이 hole 이 발생하는 것을 확인할 수 있습니다.

backward mapping

위에서 얘기한 hole 을 방지하기 위한 방법 중 하나로 backward warping 이란 것이 있습니다. forward warping 에서 src 의 좌표를 기준으로 dst 의 좌표를 계산했다면, backward warping 에서는 dst 의 좌표를 기준으로 src 의 좌표를 계산하게 됩니다.
간단하게 pseudo code 로 표현하면 아래와 같이 되겠습니다.

간단히 코드만 봐도 예상할 수 있겠지만 backward_warping 을 해주게 되면 hole 은 확실하게 없앨 수 있습니다. 결과 이미지는 아래와 같은데, 아주 깔끔한 결과가 나오지는 않았습니다.

forward (or backward) warping with interpolation

forward warping 을 하게 되면 hole 이 생기게 되고, 단순한 backward warping 을 하게 되면 이미지의 화질 저하가 발생하게 되는데, interpolation 을 사용하게 되면 이를 조금 더 개선할 수 있습니다.

전 linear-interpolation 을 사용해보았는데, 설명하기는 복잡하니 관심있으신 분은 저 아래 첨부할 소스를 참고해보시면 좋겠습니다. 결과는 아래와 같이 나옵니다.

우선 interpolation 을 이용한 forward warping 입니다. 복잡하게 하기는 귀찮고 해서 대강 구현했더니, hole 이 줄기는 했지만 여전히 존재하고 있습니다.

다음은 backward warping 에 linear interpolation 을 적용한 결과입니다. hole 도 없고, 보기에 상당히 괜찮아진 것을 확인할 수 있습니다.

소스코드:
https://github.com/Tee0125/snippet/tree/master/perspective_projection
참고자료:
http://en.wikipedia.org/wiki/Perspective_%28graphical%29
http://en.wikipedia.org/wiki/Gaussian_elimination
p.s) 부동 소숫점 연산에서 x – x/x*x = 0 이라는 것이 보장되질 않더군요. 코드 한 줄 줄일려다가 디버깅을 30분동안 해야했습니다. -_ㅜ

matrix multiply with mmx #2


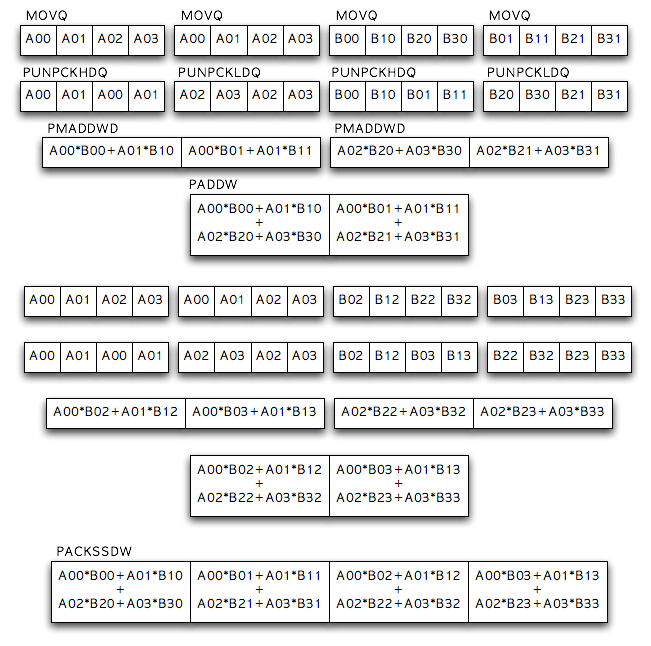
대강 생각을 해보니 정말 mmx 를 이용해서 빠르게 연산을 하려면 위와 같이 하는게 가장 빠르겠군요. 다만 레지스터를 많이 쓰고 완전히 asm 코딩을 해야한다는 게 조금 귀찮겠군요. 😉
위의 다이아그램에 있는 과정을 통해 4×4 matrix * 4×4 matrix 의 한 row 씩을 계산해낼 수 있습니다. 대강 계산했을 때 3배 이상의 속도 향상이 있을거라고 예상되던데 과연~

코드로 옮기니 위와 같군요. 중간에 실수로 바이트오더를 헷갈려서 연산 결과가 뒤집혔었습니다. 정상적인 결과는 250 260 270 280 이 나와야 하는데 280 270 260 250 이 나와버리더군요. 아아 이거 다시 하고 싶은 작업이 아니네요;
흐흣 그래도 오랫만에 어셈블리 관련된 것들을 생각하고 있는데, 이것도 가끔 하니까 재밌네요. 근데 길어지면 할만하지 않다는거 -_-!
p.s) 전체 연산 코드를 보고 싶으시면 http://mytears.org/resources/mysrc/c/mmx.c 를 보시길 😉

matrix multiply with mmx #1

몇 일 전에 썼던 글에서 테스트를 해본 내용을 바탕으로 4×4 matrix multiply 연산을 mmx 를 이용해서 구현해봤습니다.

위와 같은 c version 의 코드를 작성한 후 아래와 같은 asm version 으로 컨버팅을 해봤는데, 100000 번 반복해서 연산을 하도록 해본 결과 mmx 버젼이 c 버젼보다 3배 정도 빠르게 연산을 하는 것을 확인할 수 있었습니다. (-O0 옵션과 함께 컴파일 했을 경우)
하지만 -O3 옵션과 함께 컴파일하게 되면 asm 버젼은 무한룹에 빠진 듯한 모습을 보여줬고, c 버젼의 수행속도가 -O0 로 컴파일한 asm 버젼보다 빠른 현상이 발생했습니다. 이유는 알 수 없음 -_-;

8×8 matrix 는 뭔가 좀 더 생각해야할 것 같으니 나중에 정말 필요한 일 있을 때 구현을 해봐야겠습니다. -_-;
inline asm 작업을 하면서 eax 레지스터 값을 백업하지 않고 저렇게 사용해도 되는지는 잘 모르겠지만 –;; 하여튼 저 코드에 한해서는 별 문제 없으니 패스~ 꺄홋!!