만약 서로 다른 2개의 (x,y) 쌍을 가지고 있다면 아래와 같은 직선의 방정식을 계산해낼 수 있습니다.
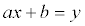
이를 아래와 같은 매트릭스 형태로 표현할 수도 있습니다.
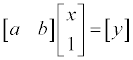
그런데 (x,y) 값을 2 쌍보다 더 많이 알고 있다면, 해가 구해낼 수 없게됩니다. 이를 over constraint 라고 하며, over constraint 상태에서 가장 에러가 작은 직선의 방정식을 구해내는 것을 line fitting 이라고 부릅니다.
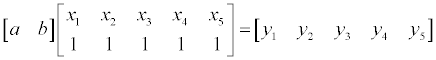
line fitting 을 하는 방법은 크게 2가지 방법이 있습니다. 첫번째는 에러를 최소화 하는 계수 a, b 를 찾기 위해 편미분을 이용하는 것이고, 두번째로는 pseudo inverse 를 이용하는 방법입니다.
line fitting with differencial equation
편미분을 통해 최적의 직선을 찾아내기 위해 우선 Error 를 아래와 같이 정의해 봅시다.
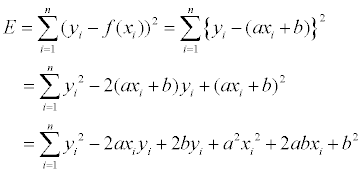
2차 곡선의 최소값은 기울기가 0이 되는 지점에 있으므로 a, b 각각에 대해 편미분을 한 뒤 기울기가 0 이 되는 지점을 찾습니다.
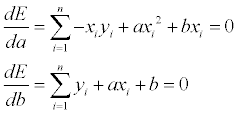
위 식을 정리하면 아래와 같은 매트릭스로 표현이 가능하며,
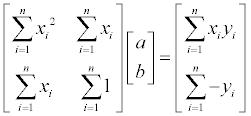
역함수를 양 변에 곱해주게 되면 간단히 계수 a, b 를 구할 수 있게 됩니다.
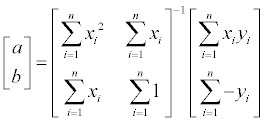
line fitting with pseudo inverse
지금까지 편미분을 이용한 line fitting 을 알아봤는데, 이 경우는 손으로 계산해야하는 것들이 많았지만 pseudo inverse 를 이용하면 계산을 모두 컴퓨터에게 맡길 수 있기 때문에 훨씬 쉽게 직선의 방정식을 구할 수 있습니다.
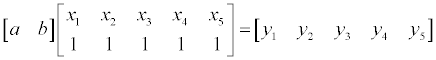
pseudo inverse 를 이용한 방법을 알아보기 앞서 위 매트릭스를 간단히 아래와 같이 표현하기로 하겠습니다.
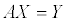
X 에 대한 inverse 를 계산할 수 있다면 간단하게 계수 a, b 를 구할 수 있겠지만 불행히도 X 는 inverse 를 가지지 못하기 때문에 X 에 자신의 transpose 를 곱해준 뒤 역행렬을 구하는 방법을 사용하게 되며, 이런 식으로 역행렬을 구해내는 방법을 pseudo inverse 라고 합니다.
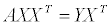
식을 정리하고 나니 아래와 같은 간단한(?) 행렬 연산을 통해 계수 a, b 를 계산해낼 수 있겠습니다.
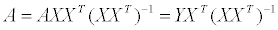
Result
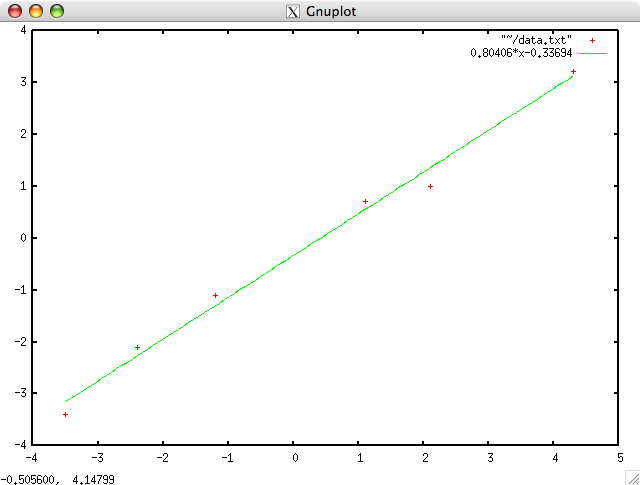
아래 그래프는 (1.1,0.7), (2.1,1.0), (4.3,3.2), (-1.2,-1.1), (-2.4,-2.1), (-3.5,-3.4) 이렇게 6개의 점에 대한 line fitting 결과를 gnuplot 을 이용해서 그래프로 만든 것이며, 6개의 점 사이를 지나는 직선이 구해진 것을 쉽게 확인할 수 있겠습니다.
p.s) 매트릭스 관련된 오퍼레이션들을 다 짜놨더니 이거이거 이런 간단한 것들 돌려보는건 일도 아니네요. 요 근래 뭔가 조급해하고 있었는데, 맘잡고 기초부터 탄탄히 해놓는게 나을 거 같다는 생각이 들어서. 욕심을 줄이고 있습니다. 후훗
코드: https://github.com/Tee0125/linear_regression/blob/master/numpy/numpy_linear_regression.py