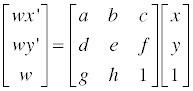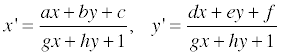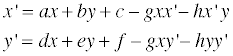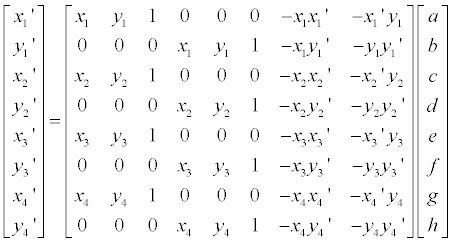팩스에서 처럼 이미지를 흑/백 으로만 표현할 수 있는 경우에도 어느 정도의 명암을 표현하기 위한 방법으로 아래와 같은 오리지널 이미지가 있을 때…

한 픽셀 값은 0~255 사이의 값을 가진다고 하고, 128 이상의 값은 하얀 색으로, 128 미만 값은 검은 색으로 표현하면 결과는 다음과 같다.

보다시피 디테일은 거의 사라져버리기 때문에 이런 것을 피하기 위해 디더링이란 기법을 사용하곤 한다. 수식으로 이를 표현해보자면 다음과 같고…
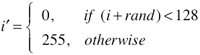
말로 설명하자면 랜덤 값을 더해준 뒤 128 을 기준으로 Thresholding 을 한다! 정도로 표현이 가능할 듯… 이론적으론 매우 간단하지만 효과는 확실하다. -16~16 의 랜덤 값을 이용하여 dithering 한 결과는 다음과 같다.
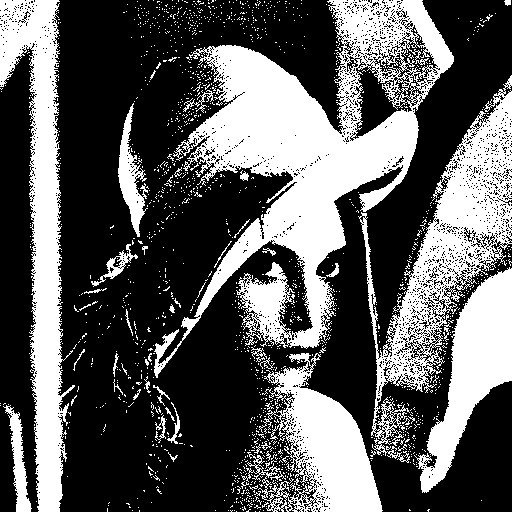
-32~32 사이의 랜덤 값을 이용할 경우는…
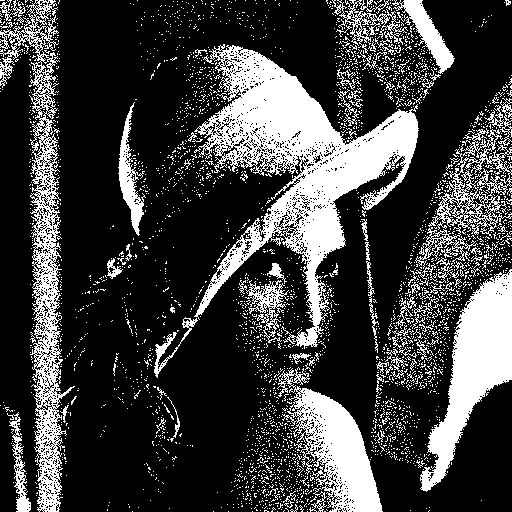
확실히 좀 디테일이 조금 생겨나는 것을 확인할 수가 있다. 장비들이 좋아지면서 이런 식의 트릭들에 대한 연구는 사라져가는 것 같다. -_ㅠ
위 테스트에 사용한 코드:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
#include <stdio.h> #include <time.h> #include <stdlib.h> int main( int argc, char** argv ){ int i, j; unsigned char* src; unsigned char* dst; FILE* in; FILE* out; src = (unsigned char*)malloc(sizeof(unsigned char)*512*512); dst = (unsigned char*)malloc(sizeof(unsigned char)*512*512); srand(time(NULL)); in = fopen("lena512.raw", "rb" ); fread( src, sizeof(unsigned char), 512*512, in ); fclose(in); for( j = 0 ; j < 512 ; j++ ){ for( i = 0 ; i < 512 ; i++ ){ if( src[j*512+i] > 128 ) dst[j*512+i] = 255; else dst[j*512+i] = 0; } } out = fopen("lena512_thres.raw", "wb" ); fwrite( dst, sizeof(unsigned char), 512*512, out ); fclose(out); for( j = 0 ; j < 512 ; j++ ){ for( i = 0 ; i < 512 ; i++ ){ if( (src[j*512+i] + rand()%32 - 32) > 128 ) dst[j*512+i] = 255; else dst[j*512+i] = 0; } } out = fopen("lena512_dither_32.raw", "wb" ); fwrite( dst, sizeof(unsigned char), 512*512, out ); fclose(out); return 0; } |