HCI 과제 덕에 심심찮게 프로그래밍을 하게 되네요. 첫 과제 였던 3D rotation 관련을 구현하는 것도 상당히 흥미로웠지만, 두번째 과제인 Perspective Projection 를 구현하는 것은 정말 멋진 경험이었다고 생각합니다.
지난 며칠간 꽤나 재밌게 프로그래밍을 했던 관계로 블로그에도 살짝 정리해보는게 어떨까 하는 생각이 들었는데, 막상 쓸려니 내용이 잘 전해질지 의문이네요.
What is the Perspective Projection?
Perspective Projection 이란 아래의 왼쪽 이미지를 오른쪽 이미지 처럼 변화시키는 것을 얘기합니다. 꼭 저렇게 비뚜러진 이미지를 바로잡는것은 아니고, 이미지가 투영되는 면을 변화시키는 것이라고 생각하시면 됩니다.

이해를 돕기 위해 wikipedia 에서 이미지를 하나 가져왔습니다. 아래 이미지의 연보라색 면이 상이 맺히는 곳이라고 할 때, perspective transform 은 그 보라색 면을 이동시킨 것 같은 효과를 주기 위해 사용합니다.
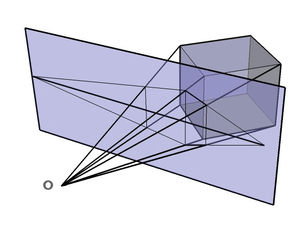
How to get a projection matrix.
기본 적으로 Perspective Transform 을 위한 식은 다음과 같습니다.
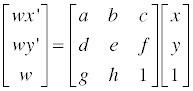
homogenious coordinate 를 사용하고 있으니 x’ 와 y’ 에 관한 식은 아래와 같이 바꿔쓸 수 있습니다.
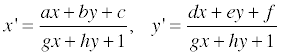
이를 정리하면 다음과 같은 꼴로 만들 수 있고,
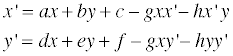
우리가 값을 알고 싶은 변수들은 a, b, c, d, e, f, g, h 이렇게 8 개이므로, (x, y) 와 그에 대응되는 (x’, y’) 쌍을 4개만 알고 있으면 projection matrix 를 구할 수 있습니다. 이를 구하기 위한 매트릭스는 아래와 같습니다.
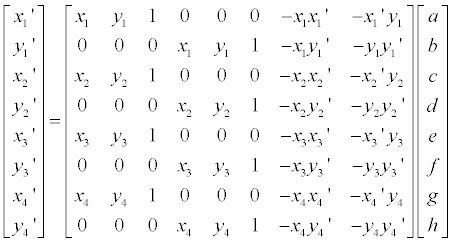
남은 건 8×8 matrix 의 inverse matrix 를 구한 뒤 뒤 쪽의 매트릭스에 곱해주는 것 뿐이군요.
Implementation of Perspective projection
이제까지 Perspective Transform 을 위한 매트릭스에 대해 알아봤습니다. 이제는 실제 구현을 해보는 것만 남았네요. 위에서 알아봤듯이 Perspective matrix 를 구하려면 matrix multiplication 과 inverse 를 위한 인터페이스가 필요합니다.
matrix multiplication 의 경우 서로 곱할 수 있는 형식인지를 체크한 뒤 단순한 계산을 하면 되고, inverse 는 gauss elimination 을 이용 reduced row echelon form 으로 만들어주는 것을 통해 쉽게(?) 구해낼 수 있습니다.
위의 두 가지까지 구현했다면, 이제 warping 만을 구현하면 되겠습니다. 이 warping 은 크게 두가지 방법을 통해 구현할 수 있습니다.
forward mapping
forward mapping 은 말 그대로 src 의 x, y 좌표에 대하 dst 의 x’, y’ 를 계산 한 뒤 값을 채워주는 방식입니다. 간단히 pseudo code 로 표현하면 다음과 같이 표현할 수 있겠네요.
|
1 2 3 4 5 6 7 |
for( y = 0 ; y < height ; y++ ){ for( x = 0 ; x < width ; x++ ){ x' = (ax+by+c) / (gx+hy+1); y' = (dx+ey+f) / (gx+hy+1); dst[y'][x'] = src[y][x]; } } |
근데 막상 구현을 해놓고 보면 pixel 이 정수단위이기 때문에 아래와 같이 hole 이 발생하는 것을 확인할 수 있습니다.

backward mapping
위에서 얘기한 hole 을 방지하기 위한 방법 중 하나로 backward warping 이란 것이 있습니다. forward warping 에서 src 의 좌표를 기준으로 dst 의 좌표를 계산했다면, backward warping 에서는 dst 의 좌표를 기준으로 src 의 좌표를 계산하게 됩니다.
간단하게 pseudo code 로 표현하면 아래와 같이 되겠습니다.
|
1 2 3 4 5 6 7 |
for( y' = 0 ; y' < height ; y'++ ){ for( x' = 0 ; x' < width ; x'++ ){ x = (ax'+by'+c) / (gx'+hy'+1); y = (dx'+ey'+f) / (gx'+hy'+1); dst[y'][x'] = src[y][x]; } } |
간단히 코드만 봐도 예상할 수 있겠지만 backward_warping 을 해주게 되면 hole 은 확실하게 없앨 수 있습니다. 결과 이미지는 아래와 같은데, 아주 깔끔한 결과가 나오지는 않았습니다.

forward (or backward) warping with interpolation
forward warping 을 하게 되면 hole 이 생기게 되고, 단순한 backward warping 을 하게 되면 이미지의 화질 저하가 발생하게 되는데, interpolation 을 사용하게 되면 이를 조금 더 개선할 수 있습니다.
전 linear-interpolation 을 사용해보았는데, 설명하기는 복잡하니 관심있으신 분은 저 아래 첨부할 소스를 참고해보시면 좋겠습니다. 결과는 아래와 같이 나옵니다.
우선 interpolation 을 이용한 forward warping 입니다. 복잡하게 하기는 귀찮고 해서 대강 구현했더니, hole 이 줄기는 했지만 여전히 존재하고 있습니다.

다음은 backward warping 에 linear interpolation 을 적용한 결과입니다. hole 도 없고, 보기에 상당히 괜찮아진 것을 확인할 수 있습니다.

소스코드:
https://github.com/Tee0125/snippet/tree/master/perspective_projection
참고자료:
http://en.wikipedia.org/wiki/Perspective_%28graphical%29
http://en.wikipedia.org/wiki/Gaussian_elimination
p.s) 부동 소숫점 연산에서 x – x/x*x = 0 이라는 것이 보장되질 않더군요. 코드 한 줄 줄일려다가 디버깅을 30분동안 해야했습니다. -_ㅜ