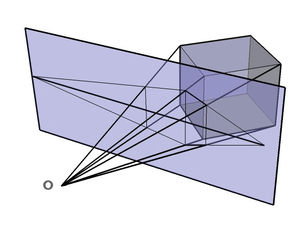
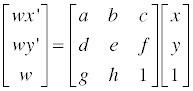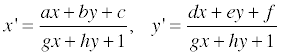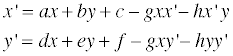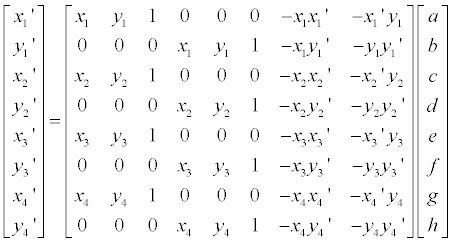며칠 전 Perspective Projection 을 정리해놓은 김에 3D Image Rotation 도 정리를 해볼까 싶습니다.
Rotation Matrix
3D 이미지 회전은 아래와 같은 행렬을 통해 새로운 좌표를 계산할 수 있습니다. 또한 이 행렬들은 모두 unitary matrix 이기 때문에 Transpose 를 취해줌으로 역행렬을 쉽게 구할 수 있습니다.
z축 기준: (xy 평면에서의 회전)
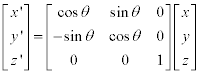
y축 기준: (zx 평면에서의 회전)
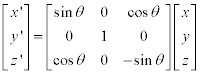
x축 기준: (yz 평면에서의 회전)
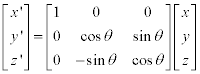
Implementation of Image Rotation
처음에는 3차원 공간을 3차원 배열을 사용하여 모델링한 뒤 실제 3차원 좌표를 모두 뒤지며 forward/backward mapping 하는 방법을 통해 3D image rotation 을 구현해보았습니다. 3차원 배열을 이용 512×512 사이즈의 lena image 를 회전시키려면 (512*1.414)^3 만큼의 공간이 필요하게 되고, 저 공간을 모두 뒤지려면 계산 복잡도가 엄청나더군요.
실제 이 방법을 통해 이미지를 회전 시키는 데 ‘분’ 단위 시간이 필요했던 것으로 기억합니다. 게다가 변환을 반복할 수록 이미지의 디그라데이션이 심해졌기 때문에 이건 아니라는 생각이 들더군요. 이런 경우 이미 잘 설계되어 있는 그래픽 라이브러리를 참고하는 것이 좋기 때문에 OpenGL 의 인터페이스를 살펴보며 어떤 식으로 구현하면 좋을 지 생각하기 시작했습니다.
뭐 어짜피 화면이나 이미지로 보여주기 위해선 2D 평면에 projection 하는 것이 필요하므로 매 번 이미지 자체를 돌리기 보다 축을 회전시키고, 마지막에 그 축을 이용해서 원래 이미지를 새로운 좌표 공간으로 매핑시켜주면 되겠다는 결론을 얻었습니다.
우선 x, y, z 좌표를 identity matrix 로 표현한 뒤 R^T * AXIS 를 통해 새로운 축 AXIS’ 를 구할 수 있고, 회전을 시키고 싶은 만큼 위 연산을 반복해준 뒤 forward mapping 을 해주는 것으로 빠르고 훌륭한 품질을 보여주도록 구현하는걸 성공했습니다.
위 이미지는 512×512 사이즈의 lena 이미지를 z축을 기준으로 45도만큼 회전시킨 결과입니다. 왼 쪽은 단순히 forward mapping 을 해준 것이고 오른쪽은 weighted sum 을 이용해서 forward mapping 을 개선해준 것입니다.
결과적으로 Photoshop 등을 이용한 만큼 훌륭한 이미지를 얻어낼 수 있는 것을 확인할 수 있습니다.
Other Results
아래 이미지는 x 축, y축, z축을 기준으로 순서대로 30도씩 회전시킨 이미지입니다. 이런 식으로 계산을 하려면 순서를 뒤집어서 z축, y축, x 축 기준으로 30도씩 회전을 시켜주면 됩니다.
다음은 x축으로 30도, y축으로 60도 만큼 돌린 결과

실제 구현 코드에 관심이 있으신 분들은 아래 링크를 방문하시면 되겠습니다. 이런 걸 하나하나 구현해볼 때마다 느끼는 거지만 openGL 같은 라이브러리를 설계하신 분들은 상상하기 힘들 정도로 똑똑한 것 같아요.
소스:
https://github.com/Tee0125/snippet/tree/master/rotation3d